FQT
Overview
FQT utilizes the same pivot at the same level. Fig. 1 shows an example of FQT, where o1 is used for the first level, and o6 is used for the second level. FQT is also an unbalanced tree. Hence, FHQT is proposed, where objects are stored in the leaves and all the leaves are at the same level. In addition, FHQT can be also stored as FQA using an array/table structure. Note that, FQA and LAESA are the same. Note that, although FQT is designed for discrete distance function, it can also be extended to support continuous distance function similar as BKT.
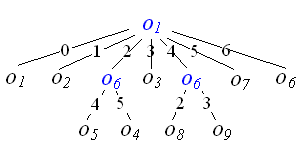
Fig. 1 Example of FQT